在微分几何错综复杂的图景中，“度量”的概念是其基石，它提供了我们测量和感知几何属性的根本框架。度量张量，通常简称为“度量”，远不止是一个抽象的数学构造，它赋予了流形距离、角度和体积的意义，有效地将一个裸露的拓扑空间转化成一个完全实现的几何空间。没有度量，流形就像一张没有尺子或量角器的画布——它有形状和连通性，但无法量化其尺寸或点之间的关系。

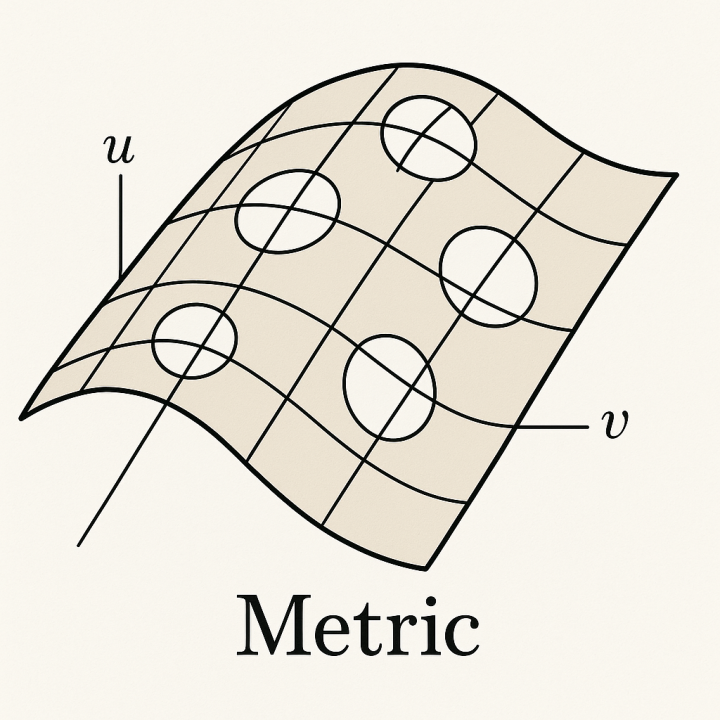
从最基本的层面来看，微分几何中的度量是流形切空间上一个平滑变化的内积。要理解这一点，让我们考虑流形 M 上的一个点 p。在这一点上，我们可以想象一个“切空间” TpM，它是一个向量空间，包含所有从 p 出发并在流形上移动的可能方向。度量 g 将 TpM 中任意两个切向量 u,v 赋予一个实数 g(u,v)。这种赋值方式满足内积的性质：它对称 (g(u,v)=g(v,u))，对两个参数都线性，并且是正定的（对于 u≠0，有 g(u,u)>0）。正定性确保了非零向量的“长度”始终为正，这是物理距离的一个关键特征。

度量所提供的最直接、最直观的测量是距离。虽然流形本身并没有点与点之间距离的概念，但度量允许我们定义切向量的长度。通过沿着曲线积分这些无穷小长度，我们可以定义曲线的长度。具体来说，对于流形上的一条参数化曲线 γ(t)，它在 t₁ 和 t₂ 之间的长度 L 由以下积分给出：

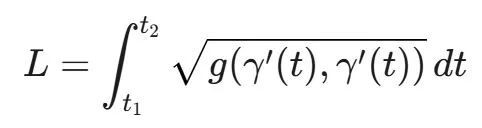
其中 γ′(t) 是曲线在 t 处的切向量。根据这个度量，流形上两点之间的“最短路径”被称为测地线。测地线将欧几里得空间中的直线概念推广到弯曲空间。例如，在球面上，两点之间的最短路径是一个大圆弧，它就是相对于标准球面度量的测地线。

除了长度，度量还测量相交曲线或切向量之间的角度。给定 TpM 中的两个切向量 u,v，它们之间的角度 θ 使用度量定义为：

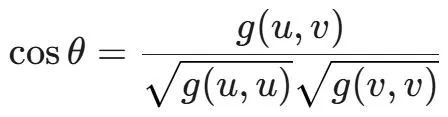
这个公式是欧几里得向量空间中点积角度公式的直接推广。这种测量角度的能力对于理解流形的局部几何至关重要，包括正交性和内在曲率的概念。

此外，度量还赋予流形体积的概念。正如度量允许我们计算一维对象（曲线）的长度一样，它也提供了计算流形内部二维曲面面积和高维区域体积的方法。这是通过度量张量的行列式来实现的。在坐标系 (x¹,…,xn) 中，度量张量的分量是 gij=g(∂/∂xi,∂/xj)。n 维流形上的体积元 dV 由下式给出：

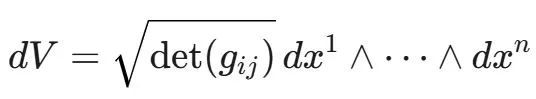
在流形的某个区域上积分这个体积元就得到了它的体积。这对于物理学中的应用至关重要，例如广义相对论中，度量决定了时空体积并影响了场和粒子的动力学。

度量还隐含地编码了流形的曲率信息。虽然曲率在将流形嵌入到更高维欧几里得空间中时是外在属性（例如，球体在三维空间中的弯曲方式），但度量允许我们定义内在曲率——一种可以纯粹从流形内部测量，而无需参考任何外部嵌入空间的属性。这是通过度量分量的导数来实现的，从而产生了黎曼曲率张量、里奇曲率和标量曲率等概念。这些张量量化了几何偏离平坦欧几里得空间的程度。例如，正曲率空间（如球体）的测地线会收敛，而负曲率空间（如马鞍面）的测地线会发散。度量是计算这些曲率测量的关键成分，这些测量对于理解流形的大尺度结构和动力学至关重要。

本质上，度量将一个纯粹的拓扑空间转换成一个可测量的几何实体。它提供了必要的机制来定义和量化我们从欧几里得几何中熟悉的所有基本几何概念，但将其推广到任意弯曲的空间。从两点之间的最短路径到区域的体积以及空间本身的内在弯曲，度量是微分几何中测量的最终仲裁者，揭示了流形几何属性的丰富而复杂的画面。它无处不在的影响使其成为从理论物理（广义相对论、弦理论）到计算机图形学和数据分析等领域不可或缺的工具。